Which Families Are Assigned to Each of the 4 Orbitals?

8.3: Electron Configurations- How Electrons Occupy Orbitals

1. Final updated

2. Save as PDF

Page ID

37944

Learning Objectives

• Derive the predicted ground-state electron configurations of atoms
• Identify and explicate exceptions to predicted electron configurations for atoms and ions
• Chronicle electron configurations to element classifications in the periodic table

Having introduced the basics of atomic structure and quantum mechanics, we tin can use our understanding of breakthrough numbers to make up one's mind how diminutive orbitals relate to one another. This allows us to decide which orbitals are occupied past electrons in each atom. The specific organisation of electrons in orbitals of an atom determines many of the chemical properties of that cantlet.

Orbital Energies and Atomic Construction

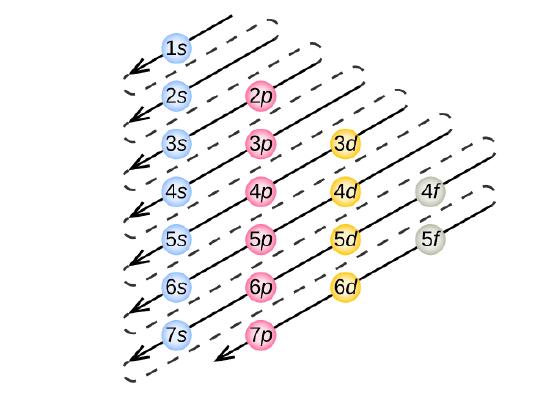
The energy of atomic orbitals increases as the primary quantum number, \(n\), increases. In any atom with two or more electrons, the repulsion between the electrons makes energies of subshells with unlike values of \(50\) differ then that the energy of the orbitals increases within a beat in the order s < p < d < f. Figure \(\PageIndex{1}\) depicts how these 2 trends in increasing energy relate. The idue south orbital at the bottom of the diagram is the orbital with electrons of lowest energy. The free energy increases equally we move upwards to the 2south and so 2p, 3south, and threep orbitals, showing that the increasing northward value has more than influence on free energy than the increasing l value for small atoms. However, this pattern does not hold for larger atoms. The 3d orbital is higher in energy than the 4s orbital. Such overlaps proceed to occur frequently as we move upwardly the chart.

Figure \(\PageIndex{1}\): Generalized free energy-level diagram for atomic orbitals in an atom with two or more electrons (not to scale).

Electrons in successive atoms on the periodic table tend to fill up low-energy orbitals get-go. Thus, many students find it disruptive that, for example, the 5p orbitals fill immediately after the 4d, and immediately before the 6s. The filling order is based on observed experimental results, and has been confirmed past theoretical calculations. Equally the principal breakthrough number, n, increases, the size of the orbital increases and the electrons spend more than fourth dimension farther from the nucleus. Thus, the attraction to the nucleus is weaker and the energy associated with the orbital is college (less stabilized). But this is not the only effect nosotros have to take into account. Within each shell, as the value of fifty increases, the electrons are less penetrating (pregnant there is less electron density plant close to the nucleus), in the lodge s > p > d > f. Electrons that are closer to the nucleus slightly repel electrons that are farther out, offsetting the more dominant electron–nucleus attractions slightly (retrieve that all electrons have −one charges, but nuclei have +Z charges). This phenomenon is chosen shielding and will be discussed in more particular in the side by side section. Electrons in orbitals that experience more shielding are less stabilized and thus higher in energy. For small orbitals (isouth through 3p), the increase in energy due to n is more significant than the increment due to 50; however, for larger orbitals the ii trends are comparable and cannot be simply predicted. We will discuss methods for remembering the observed order.

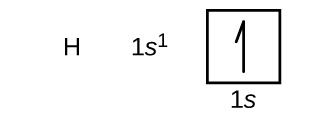
The organisation of electrons in the orbitals of an atom is called the electron configuration of the cantlet. Nosotros depict an electron configuration with a symbol that contains three pieces of information ( Figure \(\PageIndex{two}\)):

1. The number of the master breakthrough shell, n,
2. The letter that designates the orbital type (the subshell, fifty), and
3. A superscript number that designates the number of electrons in that particular subshell.

For instance, the annotation twop ^four (read "two–p–four") indicates four electrons in a p subshell (l = 1) with a chief breakthrough number (n) of 2. The notation 3d ⁸ (read "iii–d–eight") indicates viii electrons in the d subshell (i.e., l = 2) of the primary vanquish for which due north = 3.

Figure \(\PageIndex{ii}\): The diagram of an electron configuration specifies the subshell (north and l value, with letter symbol) and superscript number of electrons.

The Aufbau Principle

To determine the electron configuration for whatever particular cantlet, nosotros can "build" the structures in the order of atomic numbers. Beginning with hydrogen, and standing across the periods of the periodic table, we add one proton at a time to the nucleus and ane electron to the proper subshell until we have described the electron configurations of all the elements. This procedure is called the Aufbau principle, from the German word Aufbau ("to build up"). Each added electron occupies the subshell of everyman free energy available (in the order shown in Figure \(\PageIndex{3}\)), subject to the limitations imposed by the allowed quantum numbers according to the Pauli exclusion principle. Electrons enter higher-free energy subshells only afterwards lower-energy subshells take been filled to capacity. Figure \(\PageIndex{3}\) illustrates the traditional mode to recall the filling order for atomic orbitals.

Figure \(\PageIndex{iii}\): The arrow leads through each subshell in the appropriate filling society for electron configurations. This nautical chart is straightforward to construct. Simply make a column for all the s orbitals with each n crush on a separate row. Repeat for p, d, and f. Be certain to simply include orbitals allowed by the breakthrough numbers (no 1p or 2d, and and so forth). Finally, depict diagonal lines from top to bottom as shown.

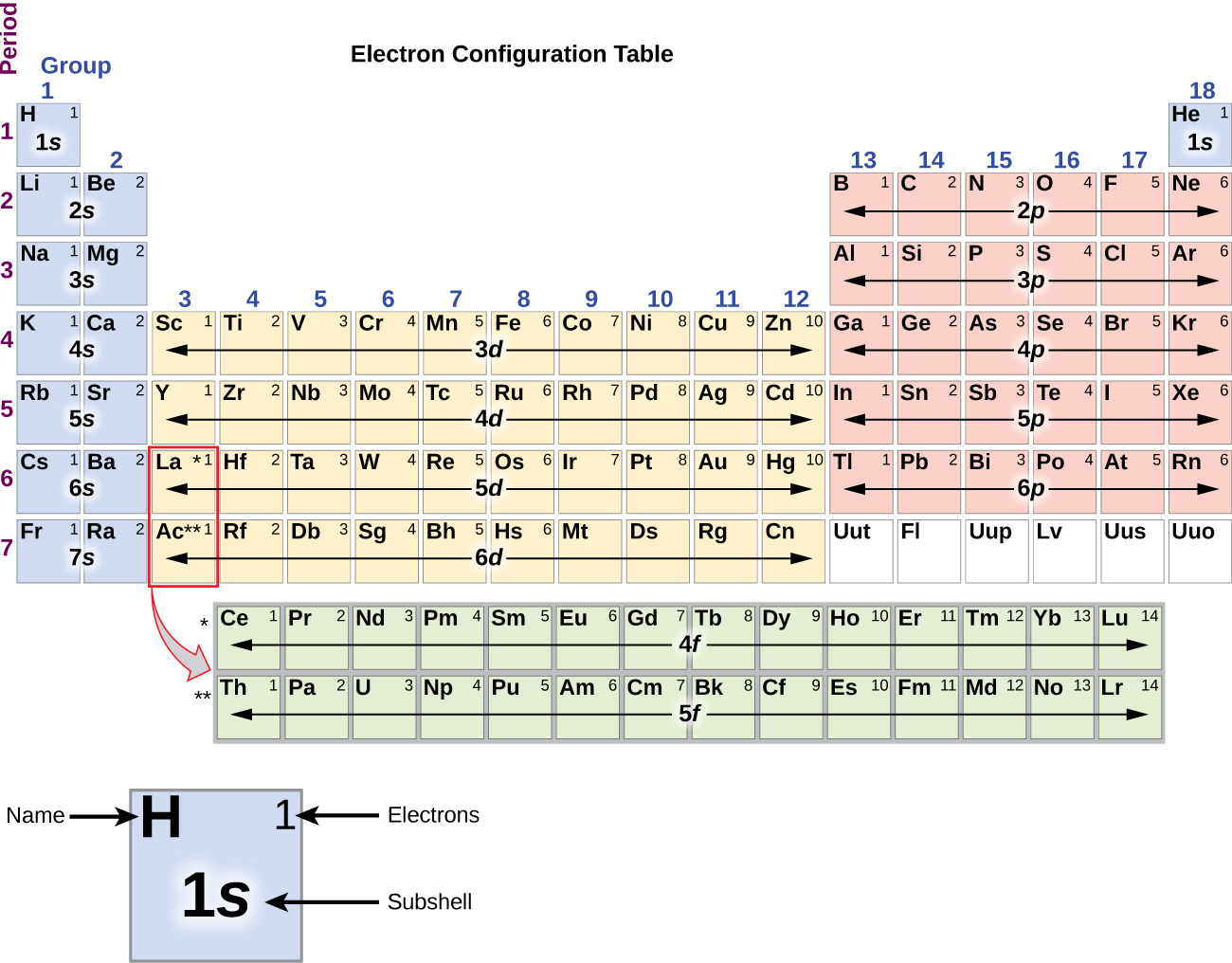
Since the organization of the periodic tabular array is based on the electron configurations, Figure \(\PageIndex{4}\) provides an alternative method for determining the electron configuration. The filling order simply begins at hydrogen and includes each subshell every bit you lot proceed in increasing Z order. For example, after filling the iiip cake up to Ar, we see the orbital will be 4s (Thousand, Ca), followed by the 3d orbitals.

Figure \(\PageIndex{4}\): This periodic table shows the electron configuration for each subshell. Past "building up" from hydrogen, this tabular array can be used to determine the electron configuration for any atom on the periodic table.

Electron Configuration of Atoms: https://youtu.exist/LlY-O3-bfnk

We will now construct the basis-state electron configuration and orbital diagram for a option of atoms in the outset and second periods of the periodic table. Orbital diagrams are pictorial representations of the electron configuration, showing the private orbitals and the pairing system of electrons. We commencement with a single hydrogen cantlet (atomic number ane), which consists of one proton and one electron. Referring to either Effigy \(\PageIndex{3}\) or \(\PageIndex{four}\), we would expect to find the electron in the 1due south orbital. By convention, the \(m_s=+\dfrac{1}{two}\) value is ordinarily filled first. The electron configuration and the orbital diagram are:

Following hydrogen is the noble gas helium, which has an atomic number of ii. The helium atom contains two protons and two electrons. The start electron has the same iv quantum numbers as the hydrogen atom electron (n = 1, fifty = 0, thou_l = 0, \(m_s=+\dfrac{1}{ii}\)). The second electron too goes into the 1s orbital and fills that orbital. The 2d electron has the same n, l, and m_l quantum numbers, just must have the opposite spin quantum number, \(m_s=−\dfrac{i}{two}\). This is in accord with the Pauli exclusion principle: No two electrons in the same atom tin can have the same set of four quantum numbers. For orbital diagrams, this means two arrows go in each box (representing two electrons in each orbital) and the arrows must point in opposite directions (representing paired spins). The electron configuration and orbital diagram of helium are:

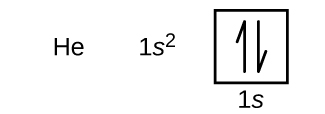
The n = 1 trounce is completely filled in a helium atom.

The next cantlet is the brine metal lithium with an diminutive number of 3. The first 2 electrons in lithium fill the 1southward orbital and have the aforementioned sets of four quantum numbers as the two electrons in helium. The remaining electron must occupy the orbital of adjacent lowest energy, the 2s orbital (Figure \(\PageIndex{iii}\) or \(\PageIndex{4}\)). Thus, the electron configuration and orbital diagram of lithium are:

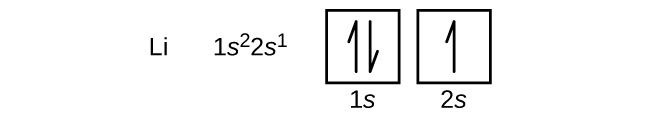
An cantlet of the element of group ii glucinium, with an atomic number of 4, contains four protons in the nucleus and 4 electrons surrounding the nucleus. The quaternary electron fills the remaining space in the 2south orbital.

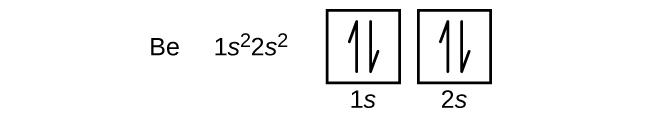
An atom of boron (atomic number 5) contains v electrons. The n = 1 beat out is filled with ii electrons and 3 electrons will occupy the n = 2 shell. Because whatever s subshell can incorporate only two electrons, the fifth electron must occupy the adjacent energy level, which will exist a iip orbital. There are iii degenerate 2p orbitals (thou₅₀ = −i, 0, +one) and the electron can occupy whatsoever 1 of these p orbitals. When drawing orbital diagrams, we include empty boxes to describe any empty orbitals in the same subshell that we are filling.

Carbon (atomic number 6) has half dozen electrons. Four of them make full the 1southward and 2s orbitals. The remaining two electrons occupy the iip subshell. Nosotros at present accept a choice of filling ane of the 2p orbitals and pairing the electrons or of leaving the electrons unpaired in two different, simply degenerate, p orbitals. The orbitals are filled as described past Hund's rule: the everyman-free energy configuration for an cantlet with electrons within a set of degenerate orbitals is that having the maximum number of unpaired electrons. Thus, the ii electrons in the carbon 2p orbitals accept identical n, fifty, and m_{due south} breakthrough numbers and differ in their thousand_l quantum number (in accord with the Pauli exclusion principle). The electron configuration and orbital diagram for carbon are:

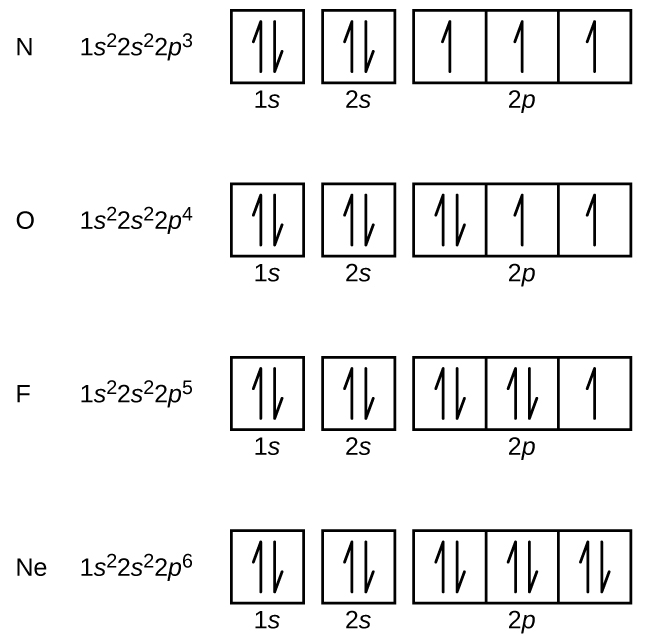
Nitrogen (atomic number 7) fills the ones and 2south subshells and has one electron in each of the three twop orbitals, in accord with Hund's rule. These 3 electrons accept unpaired spins. Oxygen (atomic number 8) has a pair of electrons in any one of the twop orbitals (the electrons have opposite spins) and a single electron in each of the other two. Fluorine (atomic number 9) has only one iip orbital containing an unpaired electron. All of the electrons in the noble gas neon (atomic number ten) are paired, and all of the orbitals in the due north = 1 and the due north = ii shells are filled. The electron configurations and orbital diagrams of these four elements are:

Figure \(\PageIndex{five}\): Since the core electron shells stand for to noble gas electron configurations, we tin abridge electron configurations by writing the noble gas that matches the core electron configuration, along with the valence electrons in a condensed format. For our sodium example, the symbol [Ne] represents core electrons, (1s ⁱⁱ2due south ²2p ⁶) and our abbreviated or condensed configuration is [Ne]iiis ^one.

The alkali metal sodium (diminutive number 11) has one more electron than the neon atom. This electron must become into the everyman-energy subshell available, the 3 s orbital, giving a one s ²2 s ^two2 p ⁶three s ¹ configuration. The electrons occupying the outermost beat out orbital(south) (highest value of north ) are called valence electrons, and those occupying the inner shell orbitals are called cadre electrons ( Figure \PageIndex5\PageIndex5). Since the cadre electron shells correspond to noble gas electron configurations, we can abbreviate electron configurations past writing the noble gas that matches the core electron configuration, along with the valence electrons in a condensed format. For our sodium example, the symbol [Ne] represents core electrons, (i due south ²2 s ⁱⁱtwo p ^vi) and our abbreviated or condensed configuration is [Ne]3 south ^one.

Figure \(\PageIndex{5}\): A core-abbreviated electron configuration (right) replaces the core electrons with the noble gas symbol whose configuration matches the core electron configuration of the other element.

Definition of Valence Electrons: https://youtu.be/_ldxOYwM2VM

Similarly, the abbreviated configuration of lithium can be represented as [He]iis ¹, where [He] represents the configuration of the helium atom, which is identical to that of the filled inner shell of lithium. Writing the configurations in this way emphasizes the similarity of the configurations of lithium and sodium. Both atoms, which are in the alkali metal family, have only one electron in a valence s subshell outside a filled set up of inner shells.

\[\ce{Li:[He]}\,2s^i\\ \ce{Na:[Ne]}\,3s^1\]

The alkaline earth metallic magnesium (diminutive number 12), with its 12 electrons in a [Ne]3s ^two configuration, is analogous to its family member beryllium, [He]2s ⁱⁱ. Both atoms have a filled s subshell exterior their filled inner shells. Aluminum (atomic number 13), with 13 electrons and the electron configuration [Ne]iiisouthward ⁱⁱ3p ¹, is analogous to its family member boron, [He]2s ⁱⁱ2p ¹.

The electron configurations of silicon (14 electrons), phosphorus (15 electrons), sulfur (16 electrons), chlorine (17 electrons), and argon (18 electrons) are analogous in the electron configurations of their outer shells to their corresponding family members carbon, nitrogen, oxygen, fluorine, and neon, respectively, except that the principal quantum number of the outer shell of the heavier elements has increased by i to n = three. Figure \(\PageIndex{six}\) shows the lowest energy, or ground-state, electron configuration for these elements every bit well every bit that for atoms of each of the known elements.

Figure \(\PageIndex{vi}\): This version of the periodic table shows the outer-shell electron configuration of each chemical element. Note that down each grouping, the configuration is often similar.

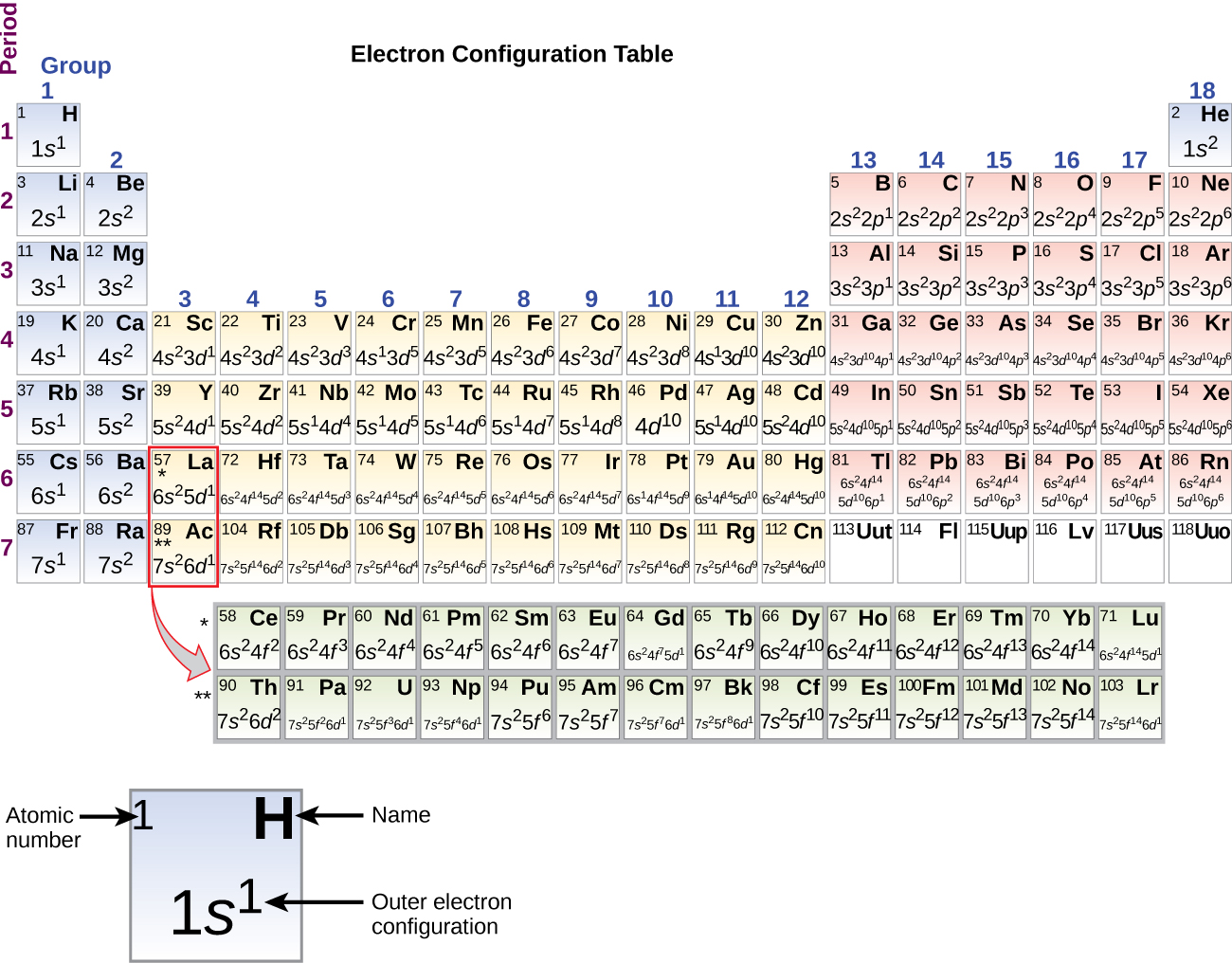
When nosotros come to the next element in the periodic table, the brine metal potassium (atomic number nineteen), we might await that nosotros would begin to add together electrons to the 3d subshell. However, all bachelor chemical and concrete evidence indicates that potassium is like lithium and sodium, and that the side by side electron is not added to the 3d level simply is, instead, added to the ivs level (Effigy \(\PageIndex{3}\) or \(\PageIndex{iv}\)). Equally discussed previously, the 3d orbital with no radial nodes is higher in energy considering it is less penetrating and more than shielded from the nucleus than the ivsouth, which has three radial nodes. Thus, potassium has an electron configuration of [Ar]4s ¹. Hence, potassium corresponds to Li and Na in its valence trounce configuration. The side by side electron is added to complete the 4s subshell and calcium has an electron configuration of [Ar]4s ². This gives calcium an outer-shell electron configuration corresponding to that of beryllium and magnesium.

Start with the transition metal scandium (atomic number 21), boosted electrons are added successively to the threed subshell. This subshell is filled to its chapters with ten electrons (call up that for l = 2 [d orbitals], there are 250 + 1 = v values of m₅₀ , meaning that there are five d orbitals that have a combined capacity of 10 electrons). The fourp subshell fills side by side. Note that for three series of elements, scandium (Sc) through copper (Cu), yttrium (Y) through silvery (Ag), and lutetium (Lu) through aureate (Au), a total of 10 d electrons are successively added to the (northward – 1) shell next to the n shell to bring that (n – 1) vanquish from eight to eighteen electrons. For ii series, lanthanum (La) through lutetium (Lu) and actinium (Ac) through lawrencium (Lr), 14 f electrons (fifty = 3, iil + 1 = 7 m_l values; thus, seven orbitals with a combined capacity of xiv electrons) are successively added to the (n – 2) beat to bring that crush from xviii electrons to a total of 32 electrons.

 Electron Configuration of Transition Metals: https://youtu.be/HzpfE0fk_E0

Example \(\PageIndex{ane}\): Quantum Numbers and Electron Configurations

What is the electron configuration and orbital diagram for a phosphorus atom? What are the four quantum numbers for the last electron added?

Solution

The atomic number of phosphorus is 15. Thus, a phosphorus atom contains 15 electrons. The club of filling of the energy levels is is, 2s, 2p, 3s, threep, 4s, . . . The 15 electrons of the phosphorus cantlet will make full upward to the 3p orbital, which volition contain three electrons:

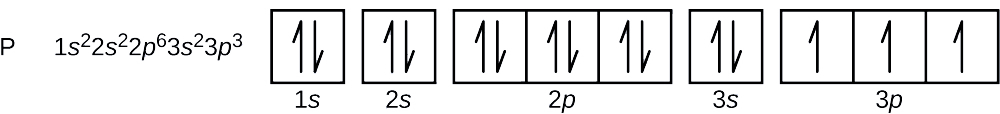
The final electron added is a 3p electron. Therefore, due north = 3 and, for a p-type orbital, fifty = i. The chiliad₅₀ value could be –1, 0, or +1. The 3 p orbitals are degenerate, so whatsoever of these g_l values is correct. For unpaired electrons, convention assigns the value of \(+\dfrac{ane}{2}\) for the spin quantum number; thus, \(m_s=+\dfrac{1}{2}\).

Exercise \(\PageIndex{ane}\)

Identify the atoms from the electron configurations given:

1. [Ar]fours ²3d ⁵
2. [Kr]vdue south ²4d ^xvp ⁶

Answer a

Mn

Answer b

Xe

Writing Quantum Number from Electron Configurations: https://youtu.be/SoUhs2_YnKU

The periodic tabular array can be a powerful tool in predicting the electron configuration of an chemical element. Still, we exercise find exceptions to the order of filling of orbitals that are shown in Figure \(\PageIndex{three}\) or \(\PageIndex{4}\). For instance, the electron configurations of the transition metals chromium (Cr; atomic number 24) and copper (Cu; atomic number 29), among others, are not those we would expect. In general, such exceptions involve subshells with very similar free energy, and minor effects can atomic number 82 to changes in the gild of filling.

In the example of Cr and Cu, nosotros find that half-filled and completely filled subshells apparently represent atmospheric condition of preferred stability. This stability is such that an electron shifts from the 4s into the iiid orbital to gain the extra stability of a half-filled 3d subshell (in Cr) or a filled 3d subshell (in Cu). Other exceptions as well occur. For instance, niobium (Nb, atomic number 41) is predicted to take the electron configuration [Kr]5south ²ivd ³. Experimentally, we find that its ground-state electron configuration is actually [Kr]5due south ¹4d ⁴. We tin rationalize this observation past maxim that the electron–electron repulsions experienced by pairing the electrons in the 5due south orbital are larger than the gap in free energy between the vs and 4d orbitals. There is no simple method to predict the exceptions for atoms where the magnitude of the repulsions between electrons is greater than the small differences in free energy between subshells.

Electron Configurations and the Periodic Tabular array

Equally described earlier, the periodic tabular array arranges atoms based on increasing atomic number so that elements with the aforementioned chemic properties recur periodically. When their electron configurations are added to the table (Figure \(\PageIndex{6}\)), we besides see a periodic recurrence of like electron configurations in the outer shells of these elements. Considering they are in the outer shells of an atom, valence electrons play the most of import role in chemical reactions. The outer electrons accept the highest free energy of the electrons in an atom and are more hands lost or shared than the cadre electrons. Valence electrons are also the determining factor in some physical properties of the elements.

Elements in any one group (or column) have the same number of valence electrons; the alkali metals lithium and sodium each take simply ane valence electron, the alkaline metal globe metals beryllium and magnesium each take 2, and the halogens fluorine and chlorine each have seven valence electrons. The similarity in chemical properties among elements of the same grouping occurs because they have the same number of valence electrons. Information technology is the loss, gain, or sharing of valence electrons that defines how elements react.

It is important to recall that the periodic table was developed on the basis of the chemical beliefs of the elements, well before any idea of their diminutive construction was available. Now we can understand why the periodic table has the system it has—the arrangement puts elements whose atoms take the aforementioned number of valence electrons in the same group. This organization is emphasized in Figure \(\PageIndex{6}\), which shows in periodic-table form the electron configuration of the concluding subshell to be filled by the Aufbau principle. The colored sections of Figure \(\PageIndex{half dozen}\) prove the three categories of elements classified by the orbitals beingness filled: main group, transition, and inner transition elements. These classifications determine which orbitals are counted in the valence vanquish, or highest free energy level orbitals of an cantlet.

1. Master group elements (sometimes called representative elements) are those in which the last electron added enters an s or a p orbital in the outermost shell, shown in bluish and cherry in Figure \(\PageIndex{6}\). This category includes all the nonmetallic elements, also as many metals and the intermediate semimetallic elements. The valence electrons for main grouping elements are those with the highest north level. For example, gallium (Ga, diminutive number 31) has the electron configuration [Ar]4south ² iiid ¹⁰ fourp ¹ , which contains three valence electrons (underlined). The completely filled d orbitals count as core, not valence, electrons.
2. Transition elements or transition metals. These are metallic elements in which the last electron added enters a d orbital. The valence electrons (those added later the terminal noble gas configuration) in these elements include the ns and (north – 1) d electrons. The official IUPAC definition of transition elements specifies those with partially filled d orbitals. Thus, the elements with completely filled orbitals (Zn, Cd, Hg, as well as Cu, Ag, and Au in Figure \(\PageIndex{6}\)) are not technically transition elements. However, the term is often used to refer to the entire d block (colored yellow in Figure \(\PageIndex{half-dozen}\)), and nosotros volition adopt this usage in this textbook.
3. Inner transition elements are metallic elements in which the last electron added occupies an f orbital. They are shown in greenish in Figure \(\PageIndex{6}\). The valence shells of the inner transition elements consist of the (northward – 2)f, the (due north – 1)d, and the ns subshells. In that location are two inner transition series:
   1. The lanthanide serial: lanthanide (La) through lutetium (Lu)
   2. The actinide serial: actinide (Ac) through lawrencium (Lr)

Lanthanum and actinium, because of their similarities to the other members of the series, are included and used to name the serial, even though they are transition metals with no f electrons.

Electron Configurations of Ions

We have seen that ions are formed when atoms gain or lose electrons. A cation (positively charged ion) forms when ane or more than electrons are removed from a parent atom. For primary grouping elements, the electrons that were added last are the outset electrons removed. For transition metals and inner transition metals, however, electrons in the s orbital are easier to remove than the d or f electrons, and then the highest ns electrons are lost, and then the (due north – ane)d or (n – two)f electrons are removed. An anion (negatively charged ion) forms when one or more electrons are added to a parent cantlet. The added electrons fill in the order predicted by the Aufbau principle.

Case \(\PageIndex{2}\): Predicting Electron Configurations of Ions

What is the electron configuration and orbital diagram of:

1. Na⁺
2. P^3–
3. Al^{two +}
4. Fe^{two +}
5. Sm^{3 +}

Solution

Start, write out the electron configuration for each parent atom. We have chosen to show the full, unabbreviated configurations to provide more than practise for students who desire it, but listing the core-abbreviated electron configurations is also acceptable.

Next, determine whether an electron is gained or lost. Remember electrons are negatively charged, so ions with a positive accuse have lost an electron. For main group elements, the final orbital gains or loses the electron. For transition metals, the final due south orbital loses an electron before the d orbitals.

1. Na: idue south ²2s ^two2p ⁶3s ¹. Sodium cation loses one electron, so Na⁺: is ²iis ²iip ⁶3s ¹ = Na⁺: 1s ²2south ^two2p ⁶.
2. P: anes ²2s ²2p ^vi3s ²3p ^three. Phosphorus trianion gains iii electrons, so P^three−: 1s ²2s ²iip ^{half dozen}3s ²3p ^six.
3. Al: 1southward ^two2s ²2p ⁶3south ²3p ¹. Aluminum dication loses two electrons Al^{2 +}: 1southward ²twos ^two2p ⁶3due south ²3p ¹ = Al^{2 +}: 1south ^two2s ²2p ^six3southward ¹.
4. Fe: onesouthward ⁱⁱ2southward ²2p ^six3s ²3p ⁶4s ²3d ^six. Iron(Two) loses ii electrons and, since it is a transition metal, they are removed from the 4s orbital Fe^{2 +}: 1due south ²2s ⁱⁱ2p ^vi3s ²3p ^{half dozen}4southward ²iiid ^{half dozen} = anedue south ²2s ⁱⁱiip ⁶iiisouth ²3p ⁶3d ^six.
5. Sm: 1south ^two2s ²2p ⁶3due south ²3p ⁶4s ²threed ¹⁰4p ⁶fives ²ivd ^x5p ^sixvis ²ivf ⁶. Samarium trication loses iii electrons. The first two will be lost from the 6southward orbital, and the concluding ane is removed from the fourf orbital. Sm^{three +}: ones ²twos ²2p ⁶3s ²3p ^half-dozen4s ²3d ^xivp ⁶5s ⁱⁱ4d ¹⁰fivep ^sixsixsouthward ⁱⁱ4f ^half-dozen = 1s ⁱⁱ2s ⁱⁱ2p ⁶threesouth ^two3p ⁶ivs ⁱⁱiiid ^x4p ^{half dozen}fives ²4d ^x5p ^six4f ^five.

Exercise \(\PageIndex{2}\)

1. Which ion with a +2 charge has the electron configuration 1s ²iis ²2p ^six3s ²iiip ⁶3d ^ten4southward ²4p ⁶4d ^five?
2. Which ion with a +3 charge has this configuration?

Answer a

Tc^{ii +}

Answer b

Ru^{3 +}

Electron Configurations of Anions: https://youtu.be/Eg6ZwdNCQrM

Electron Configurations of Cations: https://youtu.be/Y--6wNGD5Hk

Summary

The relative energy of the subshells make up one's mind the club in which atomic orbitals are filled (is, iidue south, 2p, 3s, 3p, 4due south, 3d, 4p, and and then on). Electron configurations and orbital diagrams can be determined by applying the Pauli exclusion principle (no ii electrons can accept the aforementioned fix of four quantum numbers) and Hund'south dominion (whenever possible, electrons retain unpaired spins in degenerate orbitals).

Electrons in the outermost orbitals, called valence electrons, are responsible for nigh of the chemic beliefs of elements. In the periodic tabular array, elements with analogous valence electron configurations ordinarily occur inside the aforementioned group. There are some exceptions to the predicted filling order, especially when half-filled or completely filled orbitals tin be formed. The periodic table can be divided into three categories based on the orbital in which the last electron to be added is placed: principal grouping elements (south and p orbitals), transition elements (d orbitals), and inner transition elements (f orbitals).

Glossary

Aufbau principle

procedure in which the electron configuration of the elements is determined past "edifice" them in order of diminutive numbers, calculation one proton to the nucleus and one electron to the proper subshell at a time

core electron

electron in an cantlet that occupies the orbitals of the inner shells

electron configuration

electronic structure of an atom in its ground state given as a listing of the orbitals occupied by the electrons

Hund's dominion

every orbital in a subshell is singly occupied with i electron before any 1 orbital is doubly occupied, and all electrons in singly occupied orbitals have the same spin

orbital diagram

pictorial representation of the electron configuration showing each orbital as a box and each electron as an arrow

valence electrons

electrons in the outermost or valence shell (highest value of due north) of a ground-land atom; determine how an element reacts

valence beat out

outermost beat of electrons in a basis-state atom; for primary group elements, the orbitals with the highest north level (due south and p subshells) are in the valence shell, while for transition metals, the highest energy south and d subshells brand upwards the valence shell and for inner transition elements, the highest s, d, and f subshells are included

bradleybecomeavoing.blogspot.com

Source: https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_A_Molecular_Approach_(Tro)/08%3A_Periodic_Properties_of_the_Elements/8.03%3A_Electron_Configurations-_How_Electrons_Occupy_Orbitals

Share this post